triángulos rectángulos
resolver triángulos rectángulos por medio del teorema de pitagoras:
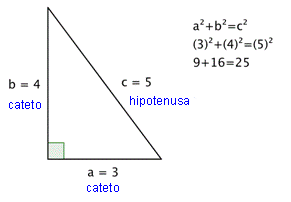
El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las respectivas longitudes de los catetos Es la proposición más conocida, entre otras, de las que tienen nombre propio de la matemática.
ejemplos:
ejemplo 1
ejemplo 2

ejemplo 3
triángulos rectángulos resueltos por medio de las razones trigonométricas:
Las Razones trigonométricas se definen comúnmente como el
cociente entre dos lados de un triangulo rectangulo asociado a sus ángulos.
Existen seis funciones trigonométricas básicas.
Para definir las razones trigonométricas del ángulo: α, del
vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este
ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los
sucesivo será:
La hipotenusa (h) es el lado opuesto al ángulo recto, o lado
de mayor longitud del triángulo rectángulo.
El cateto opuesto (a) es el lado opuesto al ángulo que
queremos determinar.
El cateto adyacente (b) es el lado adyacente al ángulo del
que queremos determinar.
Todos los triángulos considerados se encuentran en el Plano
Euclidiano, por lo que la suma de sus ángulos internos es igual a π radianes (o
180°). En consecuencia, en cualquier triángulo rectángulo los ángulos no rectos
se encuentran entre 0 y π/2 radianes. Las definiciones que se dan a
continuación definen estrictamente las funciones trigonométricas para angulos
de este rango
) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa:

El valor de esta relación no depende del tamaño del triángulo rectángulo que elijamos, siempre que tenga el mismo ángulo α , en cuyo caso se trata de triángulos semejantes.
2) El coseno de un ángulo la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa:

3) La tangente de un es la relación entre la longitud del cateto opuesto y la del adyacente:

4) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto:

5) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente:

6) La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto:
 e
e

El valor de esta relación no depende del tamaño del triángulo rectángulo que elijamos, siempre que tenga el mismo ángulo α , en cuyo caso se trata de triángulos semejantes.
2) El coseno de un ángulo la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa:

3) La tangente de un es la relación entre la longitud del cateto opuesto y la del adyacente:

4) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto:

5) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente:

6) La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto:
 e
e
ejemplo 1:

ejemplo 2:

triángulos oblicuángulos y acutángulos ley de senos y cosenos:
Teorema del seno
Ejemplo
Resolver un triángulo con los siguientes datos: a = 4 cm, b = 5 cm y B = 30º
- Dibujamos el triángulo, nombramos los ángulos y lados, colocamos los datos conocidos y resolvemos. Resolver un triángulo es decir lo que valen sus 3 ángulos y sus 3 lados.
Teorema del coseno
Ejemplo
Resolver un triángulo con los datos siguientes: a = 1200 m, c= 700 m y B = 108º
- Dibujamos el triángulo, nos dan 2 lados y el ángulo que forman.
Calculamos el lado b aplicando el teorema del coseno.
l
