Sergio Castillo Huerta NL. 5
Felix David Esquivel Moreno NL. 15
segundo grado, Grupo "3" MATUTINO.
1.1 bosquejo historico.
1.1.1 conceptos historicos trigonometricos en las diferentes culturas.
La
geometría es una de las ciencias más antiguas. Inicialmente, constituía un
cuerpo de conocimientos prácticos en relación con las longitudes, áreas y
volúmenes. En el antiguo Egipto estaba muy desarrollada, según los textos de
Herodoto, Estrabón y Diodoro Sículo. Euclides, en el siglo III a. C. configuró
la geometría en forma axiomática, tratamiento que estableció una norma a seguir
durante muchos siglos: la geometría euclidiana descrita en «Los Elementos.
El estudio
de la astronomía y la cartografía, tratando de determinar las posiciones de
estrellas y planetas en la esfera celeste, sirvió como importante fuente de
resolución de problemas geométricos durante más de un milenio. René Descartes
desarrolló simultáneamente el álgebra y la geometría analítica, marcando una
nueva etapa, donde las figuras geométricas, tales como las curvas planas,
podrían ser representadas analíticamente, es decir, con funciones y ecuaciones.
La geometría se enriquece con el estudio de la estructura intrínseca de los
entes geométricos que analizan Euler y Gauss, que condujo a la creación de la
topología y la geometría diferencial.
La
geometría en el antiguo Egipto estaba muy desarrollada, como admitieron
Heródoto, Estrabón y Diodoro, que aceptaban que los egipcios habían
"inventado" la geometría y la habían enseñado a los griegos; aunque
lo único que ha perdurado son algunas fórmulas –o, mejor dicho, algoritmos
expresados en forma de "receta"– para calcular volúmenes, áreas y
longitudes, cuya finalidad era práctica. Con ellas se pretendía, por ejemplo,
calcular la dimensión de las parcelas de tierra, para reconstruirlas después de
las inundaciones anuales. De allí el nombre γεωμετρία, geometría:
"medición de la tierra" (de γῆ (gê) 'tierra' más μετρία (metría),
'medición').
La
geometría en el antiguo Egipto estaba muy desarrollada, como admitieron
Heródoto, Estrabón y Diodoro, que aceptaban que los egipcios habían
"inventado" la geometría y la habían enseñado a los griegos; aunque
lo único que ha perdurado son algunas fórmulas –o, mejor dicho, algoritmos
expresados en forma de "receta"– para calcular volúmenes, áreas y
longitudes, cuya finalidad era práctica. Con ellas se pretendía, por ejemplo,
calcular la dimensión de las parcelas de tierra, para reconstruirlas después de
las inundaciones anuales. De allí el nombre γεωμετρία, geometría:
"medición de la tierra" (de γῆ (gê) 'tierra' más μετρία (metría),
'medición').
La
geometría en el antiguo Egipto estaba muy desarrollada, como admitieron
Heródoto, Estrabón y Diodoro, que aceptaban que los egipcios habían
"inventado" la geometría y la habían enseñado a los griegos; aunque
lo único que ha perdurado son algunas fórmulas –o, mejor dicho, algoritmos
expresados en forma de "receta"– para calcular volúmenes, áreas y
longitudes, cuya finalidad era práctica. Con ellas se pretendía, por ejemplo,
calcular la dimensión de las parcelas de tierra, para reconstruirlas después de
las inundaciones anuales. De allí el nombre γεωμετρία, geometría:
"medición de la tierra" (de γῆ (gê) 'tierra' más μετρία (metría),
'medición').
La historia
de la trigonometría y de las funciones trigonométricas podría extenderse por
más de 4000 años. Los babilonios determinaron aproximaciones de medidas de
ángulos o de longitudes de los lados de los triángulos rectángulos. Varias
tablas grabadas sobre arcilla seca lo testimonian. Así, por ejemplo, una
tablilla babilónica escrita en cuneiforme, denominada Plimpton 322 (en torno al
1900 a. C.) muestra quince ternas pitagóricas y una columna de
números que puede ser interpretada como una tabla de funciones
trigonométricas;1 sin embargo, existen varios debates sobre si, en realidad, se
trata de una tabla trigonométrica.
La historia
de la trigonometría y de las funciones trigonométricas podría extenderse por
más de 4000 años. Los babilonios determinaron aproximaciones de medidas de
ángulos o de longitudes de los lados de los triángulos rectángulos. Varias
tablas grabadas sobre arcilla seca lo testimonian. Así, por ejemplo, una
tablilla babilónica escrita en cuneiforme, denominada Plimpton 322 (en torno al
1900 a. C.) muestra quince ternas pitagóricas y una columna de números que
puede ser interpretada como una tabla de funciones trigonométricas;1 sin
embargo, existen varios debates sobre si, en realidad, se trata de una tabla
trigonométrica.
La historia
de la trigonometría y de las funciones trigonométricas podría extenderse por
más de 4000 años. Los babilonios determinaron aproximaciones de medidas de
ángulos o de longitudes de los lados de los triángulos rectángulos. Varias
tablas grabadas sobre arcilla seca lo testimonian. Así, por ejemplo, una
tablilla babilónica escrita en cuneiforme, denominada Plimpton 322 (en torno al
1900 a. C.) muestra quince ternas pitagóricas y una columna de números que
puede ser interpretada como una tabla de funciones trigonométricas;1 sin
embargo, existen varios debates sobre si, en realidad, se trata de una tabla
trigonométrica.
ejercicio:
1.- su significado etimologico es medicion de la tierrra pero en la actualidad se encarga del estudio delas figuras y suus propiredades.
R= Geometria.
2.- pueblo antiguo que se desarrollo el calculo de áreas y volúmenes para trazado de tierras y loa construcción de diques. R=Egipcios.
3.- cultura antigua que se caracterizo por el uso de figuras geométricas en sus construcciones. R= Sumerios
4.- utilizaron la rueda para fines bélicos ya descubrieron la razón en la longitud de la circunferencia y el diámetro con un valor de "3" R= Babilónicos.
5.- estabalecen el estudio de la geometria como una ciencia R= griegos
6.- lograron calcular el area de triamgulos y obtuvieron el valor PI con un valor de 3.16047 R= egipcios
7.- construyo la primera tabla de cuerdas para la solucion de triangulos R= hiparlo de nicea
8.- escirbio el almajesto, primer libro sobre astronomia y trigonometria. ademas descubrio el teorema de menelao para la solucion de triangulos esfericos R= tolomeo
9.-escribio el primer libro oxidental sobre trigonometria R= Johann Muller
10.- definieron la funcion ceno en terminos de la longitud del lado opuesto del angulo de un triangulo con hipotenusa dada R= hindues
11.- intrudujeron el triangulo polar para la solucion de triangulos esfericos y lo utilizaron en la astronomia para el calculo de tiempo astronimico R= arabes
12.- escribio el libro de la figura transversal que establece la trigonometria plana y esferica como ciencias matematicas independientes R= nasir al - din al- tusi
13.- definio las funciones trigonometricas como proporciones entre los lados de un triangulo y no como las longitudes de estos R= georjes joachim
14.- invento los logaritmos y desarollo reglas mnemotecnicas para resolver triangulos R= john napier
15.- invento el calculo diferencial integral que incorpora las funciones trigonometricas al analisis funcional R= isaac newton
16.- demostró qque las propiedades de la trigonometria son consecuencia de la aritmetica de los numeros complejos R= leonhard euler
1.2 ANGULOS
1.2.1 Definicion
Un ángulo es la parte del plano comprendida entre dos
semirrectas que tienen el mismo punto de origen o vértice.1 Suelen medirse en
unidades tales como el radián, el grado sexagesimal o el grado centesimal.
Pueden estar definidos sobre superficies planas
(trigonometría plana) o curvas (trigonometría esférica). Se denomina ángulo
diedro al espacio comprendido entre dos semiplanos cuyo origen común es una
recta. Un ángulo sólido es el que abarca un objeto visto desde un punto dado,
midiendo su tamaño aparente.
1.2.2 Unidades de medida y
conversiones
El ángulo es la región del plano comprendida entre dos
rectas que se unen en un mismo punto llamado origen. Los ángulos se calculan
siempre en sentido contrario a las agujas del reloj.
Existen principalmente dos tipos de unidades de ángulos.
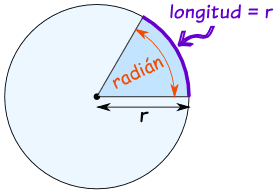
-Radián
Dibujo de la equivalencia entre ángulo radián y la
longitud del arco. El radián es una unidad de medida que se utiliza
principalmente en las matemáticas y en la física. El ángulo medido en radianes
es igual a la longitud de arco que delimitan las dos rectas si estamos en una
circunferencia de radio 1.
Una vuelta entera a una circunferencia es 2π radianes.
-Grado sexagesimal
Los grados
sexagesimales dividen una circunferencia en 360 partes iguales, de
manera que una vuelta a la circunferencia son 360º.
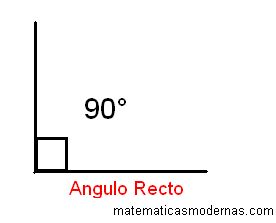
Un ángulo recto son 90º
(90 grados sexagesimales).
Los ángulos se dividen en
60 minutos (expresados con ‘) y cada uno de los minutos en 60 segundos (con”).
Por ejemplo, podríamos escribir un ángulo sexagesimal como 87º 31’ 44”. En el
mundo científico, se suelen expresar los ángulos tanto en grados, minutos y
segundos, como en radianes (aunque esta última unidad proporciona más potencia
de cálculo).
Las conversiones en los ángulos son las siguientes:
*De decimal a grados, minutos y segundos:
Sabemos que 1º=60' y 1'=60" son los factores de conversión
necesarios para esta operación.
Separamos la parte entera del número: 55,22566º quedarán 55º
0.22566º x
60'/1º=13,5396' igual tomamos como minutos solo la parte entera, ya nos va
quedando 55º13' 0,5396' x
60"/1'=32,38" y así finalmente llegamos a 55º13'32".
Así tenemos que, 55,22566º es el mismo ángulo
55º13'32" pero en la notación de grados, minutos y segundos.
*De grados, minutos y segundos a notación decimal:
En este caso sabemos que tenemos que llevar toda la
notación a grados y esto nos lleva a los siguientes factores de conversión:
1'=(1/60)º
1"=(1/3600)º o 1º=3600"
En este caso aplicamos las siguientes operaciones 55º +
13' x 1º/60' + 32" x 1º/3600" =
55,22566º.
De esta manera podemos convertir de una notación a otra
en cualquier caso, siempre usando los factores de conversión. Incluso podríamos
denotar un ángulo, todo en minutos o todo en segundos, utilizando las
conversiones, veamos cómo, con el mismo ejemplo:
55º13'32" en grados ya sabemos que es 55,22566º, si
llevamos todo a minutos tendremos:
55º x 60'/1º =
3300' +
32" x 1'/60" = 0.5333'
13'
3313,5333'.
1.2.3 Clasificación de ángulos:
Clasificación de los ángulos
Los ángulos pueden clasificarse según
su medida en cinco tipos:
angulo recto: es aquel cuya medida es de 90
Ángulo agudo: es aquel cuya medida es menor que 90°
∠ α = < 90°
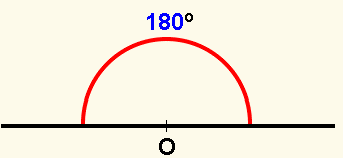
Ángulo llano: es aquel cuya medida es de 180°
∠ α = 180°
Ángulo obtuso: es aquel cuya medida es mayor que 90° y menor que
180°
∠ α = > 90° < 180º
Ángulo completo: es aquel cuya medida es de 360°
∠ α = 360°

1.2.4 Los ángulos en el
plano cartesiano
Las características de un ángulo orientado en un sistema
cartesiano son:
* Su vértice coincide con el origen de coordenadas.
* Está generado por la rotación de una semirrecta con origen
en (0;0). La semirrecta parte desde una posición inicial coincidente con el semieje positivo de las x y gira
manteniendo fijo su origen hasta llegar a una posición que marca su lado
terminal.
* El ángulo es positivo cuando está generado en sentido
contrario al movimiento de las agujas del reloj y negativo cuando está generado
en sentido horario.
*La
rotación de la semirrecta puede ser mayor que un giro.
En el gráfico se muestran
tres ángulos que tienen el mismo lado terminal:
· positivo
de 30 º (menor que un giro)
· Negativo
de 330º (menor que un giro)
· positivo
de 390º (mayor que un giro)
Se considera al plano cartesiano dividido en cuatro
sectores llamados cuadrantes:
Se determina en cuál de los cuadrantes se encuentra el lado
terminal del ángulo y esta posición da la
ubicación del ángulo. El lado terminal de los tres ángulos representados está
en el primer cuadrante por lo que todos
ellos pertenecen a dicho cuadrante.
1.3 Triángulos
El triángulo es un polígono de tres lados.
Un triángulo, en geometría, es un polígono de tres
segmentos que determinan tres puntos del plano y su limitación. Cada punto dado
pertenece a dos segmentos.1 Los puntos comunes a cada par de segmentos se
denominan vértices del triángulo2 y los segmentos de recta determinados son los
lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores
del triángulo. Un triángulo es una figura estrictamente convexa.
Un triángulo tiene tres ángulos interiores, tres pares
congruentes de ángulos exteriores, 3 tres lados y tres vértices entre otros
elementos.
Si está contenido en una superficie plana se denomina
triángulo, o trígono, un nombre menos común para este tipo de polígonos. Si
está contenido en una superficie esférica se denomina triángulo esférico.
Representado, en cartografía, sobre la superficie terrestre, se llama triángulo
geodésico.
Mediatriz:
La mediatriz de un segmento es la línea recta perpendicular
a dicho segmento trazada por su punto medio. Equivalentemente se puede definir
como el lugar geométrico — la recta — cuyos puntos son equidistantes a los
extremos del segmento. También se le llama simetral.
 Circuncentro
Circuncentro
La
mediatriz de un segmento es la línea recta perpendicular a dicho segmento
trazada por su punto medio. Equivalentemente se puede definir como el lugar
geométrico — la recta — cuyos puntos son equidistantes a lo El punto
circuncentro puede aparecer en cualquier tipo de figura geométrica que cumpla
con las reglas a explicar ya que es un trazado imaginario que se realiza sobre
algún punto de su espacio o superficie
 Mediana:
Mediana:
En
geometría las medianas (en algunos países también llamadas transversales de
gravedad[cita requerida]) de un triángulo son, cada uno de los tres
segmentos que unen cada vértice con el punto medio de su lado opuesto.
Baricentro:
el
baricentro o centroide de una superficie contenida en una figura geométrica
plana, es un punto tal, que cualquier recta que pasa por él, divide a dicho
segmento en dos partes de igual momento respecto a dicha recta.

Ortocentro:
El
ortocentro se encuentra en el interior del triángulo si éste es acutángulo;
coincide con el vértice del ángulo recto si es rectángulo, y se halla en el
exterior del triángulo si es obtusángulo. tales como la simetría.
1.3.1 Clasificación y propiedades de los triángulos de
acuerdo a la medida de sus lados
- Equilátero
Los 3
lados (a, b y c) son iguales
Los 3
ángulos interiores son iguales
- Isósceles
Tienen
2 lados iguales (a y b) y un lado distinto (c)
Los
ángulos A y B son iguales, y el otro agudo es distinto
- Escaleno
Los 3 lados son distintos
Los 3 ángulos
son también distintos
1.3.2 Clasificacion y propiedades de triangulos de acuerdo a la medida de sus ángulos.
Tipos de triángulos según sus ángulos:
· Rectángulo: contiene un ángulo un ángulo de 90º que se
encuentra enfrente de la hipotenusa.
Acutángulo: sus tres ángulos son menores de 90º.
Obtusángulo: tiene un ángulo mayor a 90º.
1.3.3
triangulos congruentes
Se
dice que dos figuras son congruentes si tiene la misma forma y el mismo tamaño.
Símbolo
de congruencia
Ejemplo de triángulos congruentes:
Postulados de congruencia
Para
dterminar si un triangulo no es congruente no es necesario comparar todos sus
elementos existen postulados quE nos permiten comprar solo algunos.
“LLL”
Dos triángulos son congruentes si sus tres lados son iguales es decir, su
longitud ide lo mismo.
“LAL” los triángulos son congruentes si dos de
sus lados son iguales y el angulo formado entre dichos lados también es igual.
“ALA” Los triángulos son congruentes si dos de sus ángulos son iguales y
el lado comprendido entre los ángulos en igual también. este ejemplo de
continuación pertenece a el postulado 1 que es “LLL”
1.3.4 semejanza de
triángulos
Concepto: Dos
triángulos son semejante cuando sus ángulos miden lo mismo sus lados pueden
tener una medida diferente. El símbolo de semejanza se denota de la siguiente manera :
Ejemplo de semejanza
de triangulos:
 Torema de tales de mileto
Torema de tales de mileto
Cuando utilizaos la semejanza de triángulos el teorema de tales de mileto adquiere masimportancia y este dice: si dos transversales cortan a varias paralelas determina en ellas segmentos correspondientes proporcionales.
Teorema de proporcionalidad
Toda paralela a un triangulo forma con los otros lados un triangulo semejante al primero.
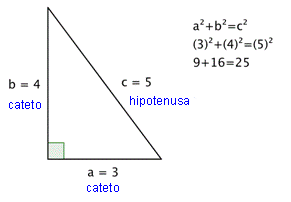
Teorema de pitagoras
El teorema
de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la
longitud de la hipotenusa es igual a la suma de los cuadrados de las
respectivas longitudes de los catetos. Es la proposición más conocida, entre
otras, de las que tienen nombre propio de la matemática.






 e
e




 e
e